Para entendernos: si invierto 100 € y tiene una rentabilidad del 10% el primer año, obtendré 110 €. Si el segundo año obtengo otro 10%, ya no será sobre 100 €, sino sobre 110 €. Es decir, una cifra mayor. La diferencia con el interés simple (sin reinvertir los intereses) es enorme. Y cuanto más largo sea el plazo, mayor será la diferencia. Supongamos una inversión inicial de 10.000 € a un tipo de interés del 8% anual. ¿Qué diferencias hay entre reinvertir los intereses o no hacerlo?
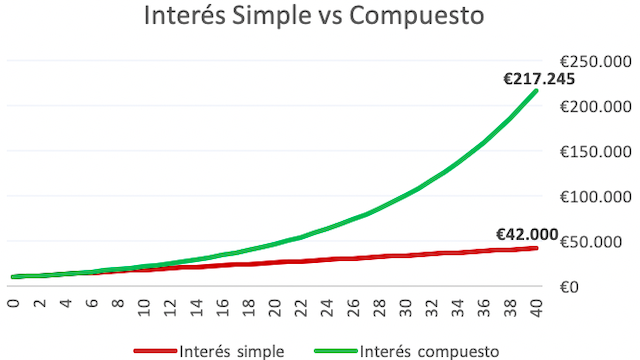
La diferencia resulta sorprendente, ¿verdad? Cuanto más elevado sea el interés y más largo sea el periodo de tiempo, la divergencia aumenta. La diferencia es que una es lineal y la otra exponencial. Repito: exponencial. Existe una fórmula conocida en el mundo de la inversión como la “Regla del 72”. Esta fórmula es muy sencilla. Consiste en dividir el número 72 por el interés que nos da la inversión. El resultado es el número de años que necesitamos para que nuestra inversión se duplique. Por ejemplo, imaginemos que la rentabilidad que esperamos obtener sea del 10% anual. Simplemente hacemos 72/10. El resultado de 7,2 es el número de años que tardará nuestra inversión en duplicarse. Fíjate bien, en poco más de 7 años duplicamos si la rentabilidad es del 10%. Efectivamente, aunque puede que no lo dijese Einstein, ni Alejandro Magno, ni Platón; el interés compuesto es una fuerza muy poderosa y la octava maravilla del mundo.
La otra maravilla es el tiempo. Existe una enorme diferencia entre aquel joven que empieza a invertir para su jubilación con 25 años, que aquel no tan joven que lo hace con 35. Supongamos que tienes 10.000 euros y eres capaz de aportar 50 euros al mes a tu ahorro, invertido en uno de los activos que tampoco ha dado tanto: el Eurostoxx (rentabilidad anualizada del periodo 31 diciembre de 2011 a 31 diciembre 2021). ¿Qué diferencias hay entre quien empieza con 25 y quién empieza con 35?
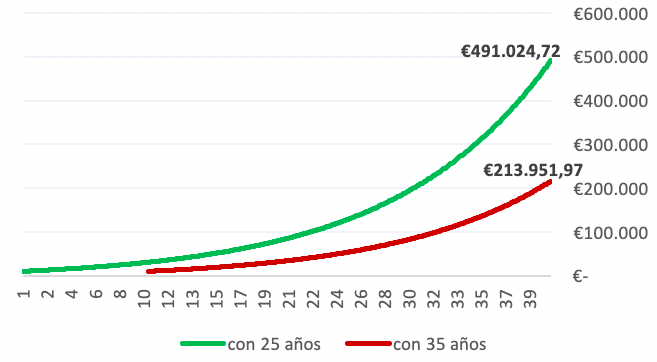
Bueno, no está mal. Una diferencia de más de 250 mil euros… Imagina si hacemos lo mismo con el Nasdaq… No te quiero decir el dato porque te daría vértigo… Y ahora, un experimento.
Según el Ministerio de Consumo (Dirección General de Ordenación del Juego), en el año 2021, cada español gastó de media casi 50 euros mensuales en juegos de azar, incluyendo la Lotería de Navidad, por supuesto. Teniendo en cuenta que el cálculo es sobre 47 millones de personas, imaginemos las cantidades que de verdad gastan los que apuestan…
Vamos a centrarnos en la Lotería de Navidad: hay 100 mil bolas, además de 180 series por número. Resumiendo, la probabilidad de acertar es de 0,00001%. Hay más probabilidades de que nazcas con 6 dedos. Por tanto, no se puede decir que “invertimos” en lotería. Por cierto, si te toca, mira bien qué haces con ese dinero (en realidad, ya lo sabes: invertirlo a largo plazo), porque lo normal es saldar una deuda, pagar la hipoteca, o algo similar. Pero si lo inviertes bien, es mucho más probable que los intereses que generes sean mayores al coste de las deudas que tienes. Pero no me quiero desviar; ni mucho menos hacerte perder la ilusión de jugar en Navidad a este impuesto que con tanta alegría pagamos. Porque nunca toca, pero a alguien le toca.
En fin, con estas pequeñas probabilidades podríamos hacer el ejercicio siguiente. Si esos 50 euros mensuales que se gastan de media en juegos de azar se invirtiesen como un ahorro periódico en tus años de vida laboral. ¿Qué sucedería? Vamos a suponer que la vida laboral es de 40 años (y viendo cómo es el sistema de pensiones, quizá me quede corto). También vamos a suponer que no sabemos en qué invertir y lo hacemos en índices. Le damos al botón de calcular y… ¡Ta-chán!

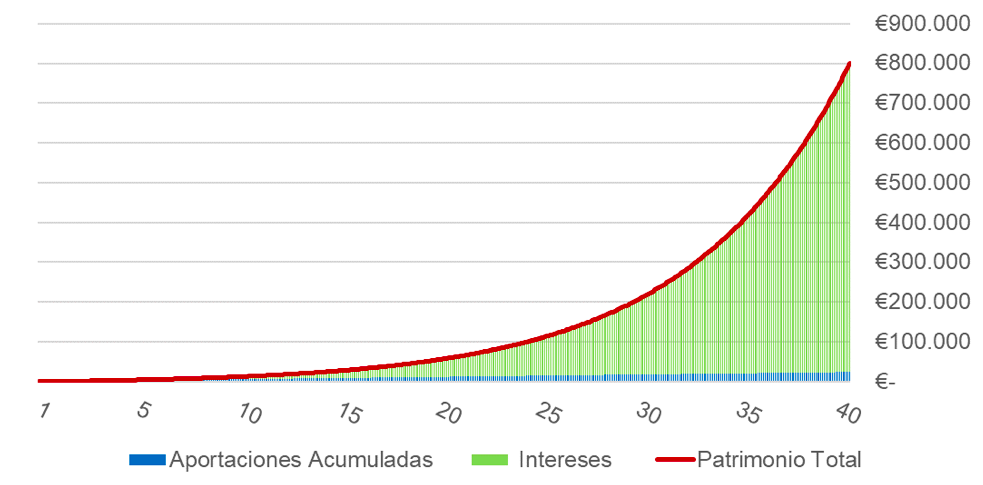
La verdad es que parece que los cálculos tienen algún error, ¿no? Pues me alegra decirte que no. En tu vida laboral es como si te hubiera tocado la Lotería de Navidad dos veces. ¡Dos veces! Pero sin correr… El dinero tienes que dejarlo invertido para dejar actuar al tiempo y al interés compuesto. Y rentabilidades pasadas no garantizan rentabilidades futuras. Quizá tu rentabilidad sea menor. Cuidado, también puede ser mayor. Y no te olvides de la inflación.
Artículo basado en el libro De Ahorrador a Inversor



¿Quieres participar en la conversación?